Introduction:
"Art of determining relative positions of objects on the surface of earth by taking measurement in horizontal and vertical planes is called surveying"
Two types of Surveying:
1) Plane surveying (Curvature of earth is not taken into consideration, For < 250 sq.m area)
2) Geodetic surveying (Curvature of earth taken into consideration, For > 250 sq.m area)
General classification of Survey:
1. According to instrument used (Chain survey, Compass survey, Plane table survey, Theodolite survey etc.)
2. According to purpose of survey (Mine survey, Geological survey, Archaeological survey, Military survey etc.)
3. According to the method employed (Triangulation survey, Traverse survey)
4. According to the place of work (Land survey, Hydro graphical or marine survey, aerial survey)
Land survey may be further divided as per below:
a) Topographical survey: for determining natural features of country and also used for artificial objects e.g. canal, railways, roads, towns & villages.
b) Cadastral survey: Performed to determine the additional details such as boundaries of fields, houses and other property.
c) City survey: Performed in connection with T.P schemes such as drainage, water supply etc. and for laying out plots, roads, streets etc.
d) Engineering survey: For collecting data for the design of engineering works such as roads, railways, reservoirs or works in connection with water supply, sewerage etc.
Done in order to ensure that errors and mistakes of one portion do not affect the remaining portion.
To fix the positions of new stations by at least two independent processes:
New stations are fixed from points already fixed by linear measurements, angular measurements of by both linear and angular measurements.
4. Vernier scale:
Similar to Diagonal scale, vernier scale is used for measuring up to second decimal.
a) Direct method:
- Pacing: Walking over a distance and counting the number of paces. Avg. length of pace is 80 cm.
(Used for reconnaissance surveys, preparation of military plans and for locating details in small scale mapping)
Passometer may be used for this method.
- Instrumental method: instruments used are Pedometer (counts steps), odometer (attached to wheel of carriage, cart, bicycle etc.), Perambulator (cart type machine to count distance)
- Judging distance: used for reconnaissance survey
- Time measurement: Distance roughly determined by knowing the avg. time taken per km by person at walk or a horse at trot and time taken to cover the distance.
- Chaining
a) Chain ( Composed of 100 or 150 pieces of galvanized mild steel wire 4mm diameter called links)
b) Arrows ( Each chain is composed by 10 arrows called marking or chaining pins, used to mark end of each chain during process of chaining, made of tempered steel wire 4mm dia and 400 mm length)
c) Tapes ( Generally used for accurate measurement of distance)
d) Ranging rods ( Used for marking positions of stations and for ranging straight lines, there are two types of ranging possible one is direct and second is indirect ranging,)
e) Line ranger (small reflecting instrument used for fixing intermediate points on the chain lines.)
Correct or true distance = (L'/L) x Measured Distance
L' = Incorrect length of a chain or tape
L = Correct length of chain or tape
- When chain used is too long, then the measured distance is too short, then error is negative and correction is positive.
- When chain used is too short, then measured distance is too long, then error is positive and correction is negative.
Direct method (Stepping method)
horizontal distances are directly measured on the ground by process of stepping consisting measuring line in short horizontal lengths as per below figure.
Indirect method
It is more accurate and rapid when slope of ground long and gentle. in this method, various slopes are measured by clinometer (usually by Abney level) or difference in elevation between successive points by level or hand level. Knowing the angle of slope of ground and slope distance, horizontal distances may be computed as per below figure.
Horizontal distances can also be determined by applying -ve corrections to the distance measured along the slope in below two cases:
Correction if vertical distances between first and last point (h) is known
correction to slope distance,
Ch = B'C' = AC' - AB'
= AB - AB'
= l - D
=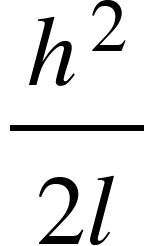 (approx)
(approx)
Correction if angle of slope of ground is known:
Ch = B'C' = AC' - AB' =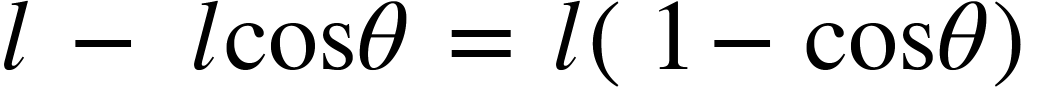
subtracting above correction will give actual horizontal distances.
errors in chaining are of following three types:
Instrumental error:
Due to faulty adjustments or imperfections of the instruments such as chain or tape may be too long or too short.
Natural errors:
Due to variations in phenomenon of nature such as temperature
Personal errors:
Classified as compensation errors and cumulative errors
Compensation errors are those which occur in either direction and tend to compensate at end. These errors do not affect survey work seriously.
Cumulative errors are those which occur in one direction only and go on accumulating. these errors do affect seriously on accuracy of survey work.

L = Measured length of a line;
l = Nominal length of a tape, and
c = Correction to the tape length
Correction may be positive or negative depending upon the correction required by tape.
Correction for temperature:
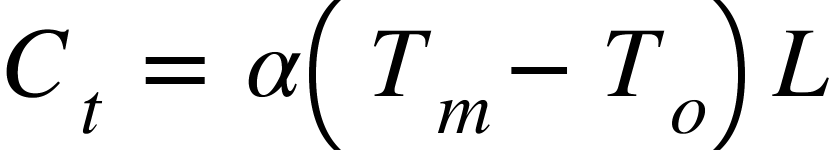 (in metre)
(in metre)
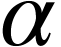 = Coefficient of thermal expansion
= Coefficient of thermal expansion
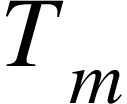 = Mean temperature during measurement
= Mean temperature during measurement
 = Temperature at which tape is standardised
= Temperature at which tape is standardised
L = Measured length in m.
so, if temperature during measurement is more then standard then correction is +ve
and if lesser then standard then correction id -ve.
Correction for pull (or tension)
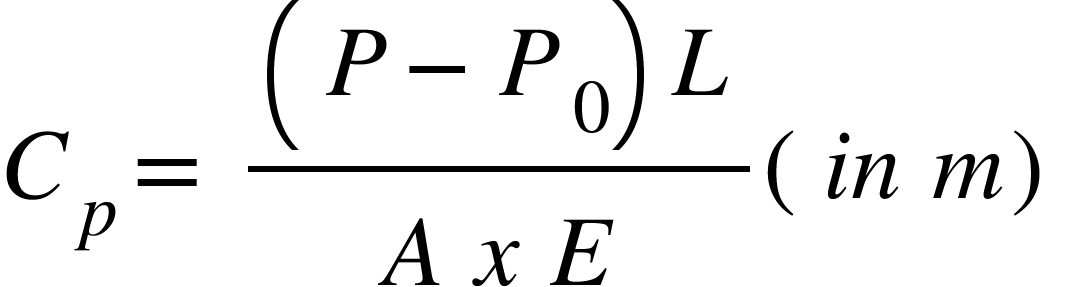
P = Pull applied during measurement in N
 = Pull at which tape is standardized in N
= Pull at which tape is standardized in N
L = Measured length in m
A = Cross-sectional area of the tape in sq.m
E = Modulus of elasticity of the tape material in N per Square m.
If P is more then then correction is +ve and if P is less then
then correction is +ve and if P is less then  then correction is -ve
then correction is -ve
Correction of sag
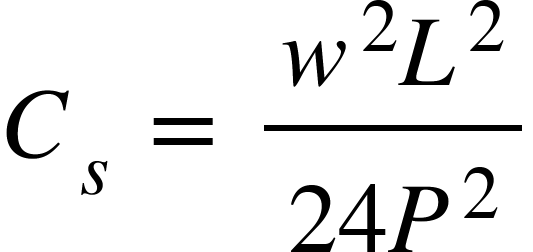
w = Weight of tape in N/m
L = Length of tape in m
P = Pull applied in N
Correction for slope or vertical alignment
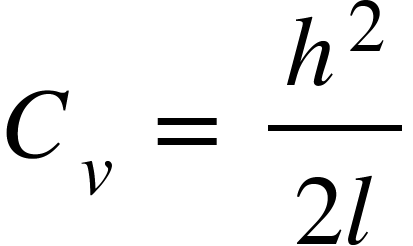
h = Difference of height between the ends of slope
l = Length of slope
If slopes are given in terms of vertical angles, then

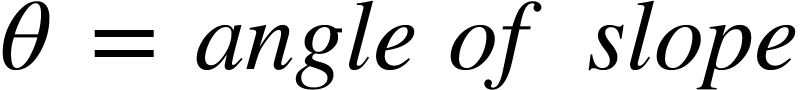
this correction is always -ve from measured length
Instruments for setting out right angles
Open cross staff:
Used for setting out an offset at at right angle
French cross staff:
Used for setting out an offset at 45 degree
Adjustable cross staff:
Used for setting out offset at any angle
Optical square:
More accurate than the cross staff and is used for setting out accurately the along offsets. it is small compact instrument based on principle of reflection. Other instrument used belonging are line ranger, box sextant and a prismatic compass.
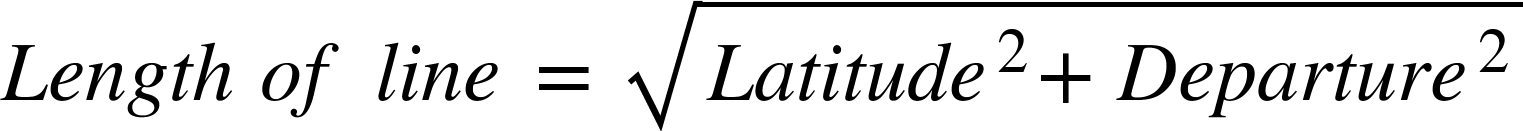

a) Topographical survey: for determining natural features of country and also used for artificial objects e.g. canal, railways, roads, towns & villages.
b) Cadastral survey: Performed to determine the additional details such as boundaries of fields, houses and other property.
c) City survey: Performed in connection with T.P schemes such as drainage, water supply etc. and for laying out plots, roads, streets etc.
d) Engineering survey: For collecting data for the design of engineering works such as roads, railways, reservoirs or works in connection with water supply, sewerage etc.
Principles of Surveying
Work form whole to part:Done in order to ensure that errors and mistakes of one portion do not affect the remaining portion.
New stations are fixed from points already fixed by linear measurements, angular measurements of by both linear and angular measurements.
Scale:
Representative Fraction (R.F):
"Ratio of Distance on map or drawing to Distance on corresponding ground"
Ex. When 1cm on map represents 10m on ground, then RF of scale is 1/1000.
Types of scale:
1. Plain scale: Used to read only two dimensions such as meters and decimeters.
Above example shows RF: 1/100 and represents 4.6m on scale of 1cm = 1m.
Accuracy is upto 0.1m (units: meter, decimeter)
2. Diagonal scale: Used to read three dimensions such meters, decimeters and centimeters.
Above example shows RF:3/200 and represents 4.56m on scale of 3cm = 2m
accuracy up to 0.01m (units: meter, decimeter, centimeter)
3. Comparative scale:
Above example shows RF:1/625000 and compares miles to kilometeraccuracy up to 0.01m (units: meter, decimeter, centimeter)
3. Comparative scale:
4. Vernier scale:
Similar to Diagonal scale, vernier scale is used for measuring up to second decimal.
Measurement of Distance:
Two methods of determining distance Direct & Indirect (computative) method.a) Direct method:
- Pacing: Walking over a distance and counting the number of paces. Avg. length of pace is 80 cm.
(Used for reconnaissance surveys, preparation of military plans and for locating details in small scale mapping)
Passometer may be used for this method.
- Instrumental method: instruments used are Pedometer (counts steps), odometer (attached to wheel of carriage, cart, bicycle etc.), Perambulator (cart type machine to count distance)
- Judging distance: used for reconnaissance survey
- Time measurement: Distance roughly determined by knowing the avg. time taken per km by person at walk or a horse at trot and time taken to cover the distance.
- Chaining
Instruments used for chaining:
a) Chain ( Composed of 100 or 150 pieces of galvanized mild steel wire 4mm diameter called links)
b) Arrows ( Each chain is composed by 10 arrows called marking or chaining pins, used to mark end of each chain during process of chaining, made of tempered steel wire 4mm dia and 400 mm length)
c) Tapes ( Generally used for accurate measurement of distance)
d) Ranging rods ( Used for marking positions of stations and for ranging straight lines, there are two types of ranging possible one is direct and second is indirect ranging,)
e) Line ranger (small reflecting instrument used for fixing intermediate points on the chain lines.)
Error in length due to incorrect chain:
Distance measured with the chain or tape of incorrect length will not be correct.Correct or true distance = (L'/L) x Measured Distance
L' = Incorrect length of a chain or tape
L = Correct length of chain or tape
- When chain used is too long, then the measured distance is too short, then error is negative and correction is positive.
- When chain used is too short, then measured distance is too long, then error is positive and correction is negative.
True area = (L'/L)^2 x Measured area
True volume = (L'/L)^3 x Measured volume
In surveying, for plotting purposes horizontal distances are required. In sloping ground it is measured in two methods as below:True volume = (L'/L)^3 x Measured volume
Chaining on sloping ground:
Direct method (Stepping method)
horizontal distances are directly measured on the ground by process of stepping consisting measuring line in short horizontal lengths as per below figure.
Indirect method
It is more accurate and rapid when slope of ground long and gentle. in this method, various slopes are measured by clinometer (usually by Abney level) or difference in elevation between successive points by level or hand level. Knowing the angle of slope of ground and slope distance, horizontal distances may be computed as per below figure.
Correction for slope
Horizontal distances can also be determined by applying -ve corrections to the distance measured along the slope in below two cases:
Correction if vertical distances between first and last point (h) is known
correction to slope distance,
Ch = B'C' = AC' - AB'
= AB - AB'
= l - D
=
Correction if angle of slope of ground is known:
Ch = B'C' = AC' - AB' =
subtracting above correction will give actual horizontal distances.
Errors in chaining
errors in chaining are of following three types:
Instrumental error:
Due to faulty adjustments or imperfections of the instruments such as chain or tape may be too long or too short.
Natural errors:
Due to variations in phenomenon of nature such as temperature
Personal errors:
Classified as compensation errors and cumulative errors
Compensation errors are those which occur in either direction and tend to compensate at end. These errors do not affect survey work seriously.
Cumulative errors are those which occur in one direction only and go on accumulating. these errors do affect seriously on accuracy of survey work.
Tape correction
Correction for absolute length:L = Measured length of a line;
l = Nominal length of a tape, and
c = Correction to the tape length
Correction may be positive or negative depending upon the correction required by tape.
Correction for temperature:
L = Measured length in m.
so, if temperature during measurement is more then standard then correction is +ve
and if lesser then standard then correction id -ve.
Correction for pull (or tension)
P = Pull applied during measurement in N
L = Measured length in m
A = Cross-sectional area of the tape in sq.m
E = Modulus of elasticity of the tape material in N per Square m.
If P is more then
Correction of sag
w = Weight of tape in N/m
L = Length of tape in m
P = Pull applied in N
Correction for slope or vertical alignment
h = Difference of height between the ends of slope
l = Length of slope
If slopes are given in terms of vertical angles, then
this correction is always -ve from measured length
Instruments for setting out right angles
Open cross staff:
Used for setting out an offset at at right angle
French cross staff:
Used for setting out an offset at 45 degree
Adjustable cross staff:
Used for setting out offset at any angle
Optical square:
More accurate than the cross staff and is used for setting out accurately the along offsets. it is small compact instrument based on principle of reflection. Other instrument used belonging are line ranger, box sextant and a prismatic compass.
Traverse surveying
Traverse surveying is one in which the framework consists of a series of connected lines whose lengths are measured with chain or tape and directions are determined with an angular instrument.
The instruments commonly used for the measurement of angles are a compass and a theodolite. sometimes, a box sextant is also used.
In traverse surveying, direction of a survey line may be defined either by the horizontal angle between the line adjacent to it or by the angle (called bearing) between the fixed line of reference (called meridian) and the line. the reference direction employed in surveying may be a true or geographical meridian, a magnetic meridian or an arbitrary or assumed meridian.
True or geographical meridian is a line in which the plane passing through the given point and the north and south poles intersects the surface of the earth. Directions of true meridians are invariable. The true meridians through the various stations are not parallel, but converge to the poles. but for small surveys, they are assumed to be parallel to each other. The horizontal angle between the true meridian and a line is called true bearing of the line. and also known as azimuth.
The Magnetic meridian is the direction indicated by a freely suspended and properly balanced magnetic needle, unaffected by local attractive forces. The angle which the line makes with the magnetic meridian is called a magnetic bearing of the line or simply bearing of the line.
The arbitrary or assumed meridian is usually the direction from a survey station to some well defined permanent object or the first line of a survey.
Systems to express bearings:
Following two systems are commonly used to express the bearings:
1. Whole Circle Bearing system
2. Quadrantal system
In Whole Circle Bearing, the bearing line is always measured clockwise from north point of reference meridian towards the line right round the circle. It may have any value between 0 to 360 degree.
Bearing observed with prismatic compass or a theodolite are WCB.
In Quadrantal system, the bearing of line is measured clockwise/anticlockwise from north or the south whichever is nearer the line, towards east or west.
In this system, bearing is reckoned from 0 to 90 degree in each quadrant.
Bearings observed with surveyor's compass are the quadrantal bearings.
Difference of Prismatic and surveyors compass
Reduced Bearings:
When the WCB of line exceeds 90, it must be reduced to the corresponding angle less than 90, which has the same numerical values of the trigonometrical functions.
Following table is used for Reduced Bearings (R.B.)
In below figure some of the examples are given
Fore and Back bearings:
Every line has two bearings, observed at each end of line.
Bearing of line in direction of progreds of survey is called fore or forward bearing (F.B.).
Bearing in the opposite direction is known as back or reverse bearing (B.B.).
It may be noted that the fore and back bearing of line differ exactly by 180 degree.
In WCB system, BB of line may be obtained from the fore bearing by following:
Back bearing = Forebearing (+/-) 180
- Sign used when Fore bearing is > 180
+ Sign used when Fore bearing is < 180
In Quadrantal system, Fore and Back Bearing are numerically equal but with opposite letters.
Ex. If F.B is N40E then B.B is S40W
Local attraction, Dip and Magnetic Declination
Magnetic needle is seriously deflected from its normal position when it is under the influence of external attractive forces. such a disturbing influence is called local attraction.
Needle will not remain in horizontal position on account of magnetic influence of earth.
It will be inclined downwards towards the pole. This inclination with horizontal is known as dip of needle. It is 0 at equator & 90 at magnetic poles.
Horizontal angle which magnetic meridian makes with true meridian is called magnetic declination or declination of needle.
Theodolite traversing:
Theodolite is most complicated and accurate instrument used for horizontal and vertical angles.
Theodolite is primarily classified as follows:
1. Transit 2. Non-transit
In Transit theodolite its telescope can revolve on vertical plane, in Non-transit theodolite telescope cant do. that is why Non transit theodolite are obsolete today.
Terms to be understood using Transit theodolite:
a) Centering: Means setting the theodolite exactly over station mark. using plumb bob
b) Transiting: Also called plunging or reversing. It is process of turning the telescope of theodolite over its supporting axis (Horizontal axis) through 180 degree in vertical plane thus bringing it upside down making it point exactly in opposite direction.
c) Line of collimation: It is also known as line of sight. imaginary line joining the point of intersection of cross hairs of the diaphragm and the optical centre of the object glass and it's continuation.
d) Axis of telescope: It is a line joining the optical center of the object glass and the centro of the eye piece. the axis of telescope must be parallel to the line of collimation.
e) Axis of level or bubble tube: It is the straight line tangential to the longitudinal curve of the level tube at the center of the tube. axis of bubble must be perpendicular to the vertical axis.
Traverse computation:
In survey work, after field work is over, positionof different points are plotted on plan with reference to two lines which are respectively parallel and perpendicular to the meridian.
These projections are called Latitude and Departure of line respectively. Latitude is defined as distance measured parallel to meridian (North or South), and Departure is defined as distance measured perpendicular to the meridian (East or West).
In Latitude Measured upward called Northing assumed to be +ve.
Latitude Measured downward called Southing assumed to be -ve.
In Departure Measured Right side called Easting assumed to be +ve.
If L is length of line and θ is its reduced bearing, then
Latitude of the line = l cosθ
Departure of line = l sinθ
= Latitude x sec of reduced bearing
= Departure x cos of reduced bearing
Balancing the traverse is process of adjusting thelatitudes and departures by applying corrections to them in such a way that algebraic sm of the atitudes, and that of the departure should be each equal to zero.
Following rules can be used to balance survey
Bowditch's rule: also known as compass rule. This rules is used to balance the traverse when the angular and linear measurements are equally precise. it is most commonly used in traverse adjustment.
a). Correction to Latitude of any side
= (Length of that side/Perimeter of traverse) x Total error in latitude
b). Correction to Departure of any side
= (Length of that side/Perimeter of traverse) x Total error in departure
Transit rule: Used to balance the traverse when the angular measurements are more precise than the linear measurements.
a). Correction to Latitude of any side
= (Latitude of that side/arithmetical sum of all latitudes) x Total error in latitude
b). Correction to Departure of any side
= (Departure of that side/arithmetical sum of all latitudes) x Total error in departure
Simple leveling:
When it is required to find the difference in elevation between two points, both of which are visible from a single position of the level, then method of simple leveling is used.
Differential leveling:
When two points are too far apart, the difference in elevation between them is too great and there are obstacles between them, then a method of differential leveling is used to find difference in elevation between them.
Contouring:
Contour is defined as line joining points having same elevation.
e.g. in above figure contour interval is 25, The constant vertical distance between any two consecutive contours is called contour interval.
Methods of contouring:
Direct method: in this method, contours to be located are direct traced out in field by locating and making a number of points on each contour.
This method by radial lines is suitable for small areas where a single point in the center can command the whole area.
Indirect method: In this method, points located and surveyed are not necessarily on the contour lines but the spot levels are taken along series of lines laid over area. this method is also known as contouring by spot levels. This method is cheaper, quicker and less tedious as compared to direct method.
below three methods are used for indirect contour
a). By squares
b). By cross-sections
This method is most suitable for survey of long narrow strips such road, railway, canal etc.
i) The center
line of the strip of land is first marked
ii) Lines perpendicular to the longitudinal strip are marked
dividing the strip into equal sections
iii) The perpendicular lines are divided into equally spaced divisions, thus forming rectangular grids.
iii) The perpendicular lines are divided into equally spaced divisions, thus forming rectangular grids.
iv) Levels are taken at the intersection of the grid lines to
obtain the cross-section profile of the strip of land.
v) Contour map is plotted in the office by interpolating points
of equal elevation based on the levels taken at site.
c). By tacheometer
This method is particularly suitable when contour of hill is required.
Interpolation of contour:
Process of spacing contours proportionally between plotted ground points is termed as interpolation of contours.
There are three methods of interpolation of contour
a). By estimating (Rough method)
b). Arithmetic (Best method used for small areas where accurate results are required)
c). By graphical method
Plane table surveying:
The method in which the field work and plotting are done simultaneously is called plane tabling.
Commonly used for small and medium scale mapping of comparatively large areas where great accuracy is not required such topographical surveys.
Following four methods are used for table surveying:
a). Radiation
In this method, point is located on plan by drawing a ray from the lane table station to the point, and plotting to scale along ray.
b). Intersection
In this method, point is fixed on plan by the intersection of the rays drawn from two instrument stations.
- This method is most commonly used for locating distant and inaccessible points, locating broken boundaries, and the point which may be used subsequently as instrument stations.
c). Traversing
This method is similar to that of compass or transit traversing. used for running survey lines between stations which have been previously fixed by other method of surbeying to locate topographical details.
d). Resection
This method is used for establishing the instrument stations only. after mixing the stations, the details are located either by radiation or intersection.
Curves:
Curves are regular bends provided in the lines of communication like roads, railways etc. they are classified as below:
a) Simple curve Consists of single arc of circle connecting two straights having same radius and magnitude through-out
b) Compound curve Consists two or more simple curves having different radii bending in same direction and lying on same side of common tangent. their centers lie on same side of curve
c) Reverse or serpentine curve is made up of two arcs having equal or different radii bending in opposite directions with common tangent at their junction. their centres lie on opposite sides of curve.
d) Deviation curve is simply a combination of two reverse curves
Transition curve:
It is horizontal curve of varying radius used to connect straight line with circular curve.
Object of introducing a transition curve at each end of circular curve is as follows:
a) to obtain gradual increase of curvature from zero at tangent point to the specified quantity at junction of the transition curve with circular curve.
b) to provide satisfactory means of obtaining a gradual increase of super-elevation from zero on tangent point to the specified amount on the main circular curve.
c) to accomplish gradually the transition from the tangent to the circular curve and from the circular curve to the tangent.
Following three types of transitional curves are in common use:
i) Cubic parabola y = fx3
ii) Cubical spiral
iii) Lemniscate is ideal transitional curve & its formula is 
first two types are used on railways and highways both while third one is used on highways only.
Tacheometric Surveying:
Branch of surveying in which the horizontal and vertical distances of point are obtained by angular observations with a tacheometer is called Tacheometric survey.
Tacheometer is in general sense, a transit theodolite having a stadia telescope filled with two horizontal hairs called stadia hairs in addition to the usual cross hair.
Horizontal distance D from the vertical axis of the instrument to the staff is given by:
D = f/i x S + (f+d)
where, f = focal length of the object glass
i = interval between stadia lines
S = staff intercept
d = horizontal distance from optical center to the vertical axis of tacheometer
in equation, f/i is called multiplying constant of tacheometer whose value is generally 100
(f+d) is called additive constant and its value varies from 30 cm to 45 cm.
when an additional convex lens (anallatic lens) is provided in telescope of tacheometer, additive constant (f+d) is taken 0.
Computation of area:
Mid-ordinate rule:
Area = (h1+h2+h3+.....+hn)/n x L
where, h1,h2...hn = hight of mid ordinates
L = length of base line
n = number of equal parts
Average ordinate rule:
l = Length of baseline
n = Number of divisions
n + 1 = Number of ordinates
Trapezoidal rule:
Area = d/2 [O1+O5+2(O2+O3+O4)]
O1,O5 = First and last offsets
d = distance of ordinates
Simpson's rule:
Area = l/3 [h1+h7+4(h2+h4+h6)+2(h3+h5)]
= l/3 [h1+hn+4(Even numbered offsets)+2(odd numbered offsets)]
l = Total length of baseline














































No comments:
Post a Comment